Structural Analysis of Moment-Resistant Frame
Structural Analysis of Moment-Resistant Frame
[ Problem Statement ]
[ Finite Element Mesh ]
[ Displacements ]
[ Bending Moments and Shear Forces ]
[ Reactions ]
[ Input/Output Files ]
You will need Aladdin 2.0 to run this problem.
Figure [1] is an elevation view of a planar moment resistant frame, which is part of an industrial building constructed on a hill-side.
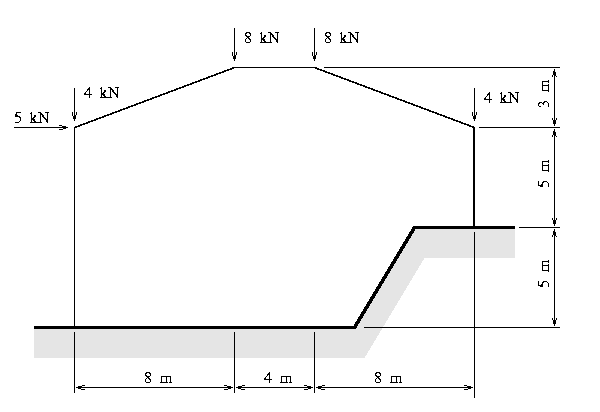
The building frame has width 20 m, and a total height of 13 m. It is constructed from steel sections having moment of inertia I = 6.6 x 10^8 mm^4 and cross section area A = 4.26 x 10^4 mm^2. The steel material has modulus of elasticity E = 200 GPa.
The building frame is subject to gravity loads, plus a moderate wind loading. We will assume that the gravity loads can be represented by point loads of 20 kN distributed over joints 2 through 4, and wind loadings can be represented by a single lateral point load of 5 kN applied to joint 2.
The building will be modeled with six nodes/joints and five beam-column elements, as labeled in Figure [2].
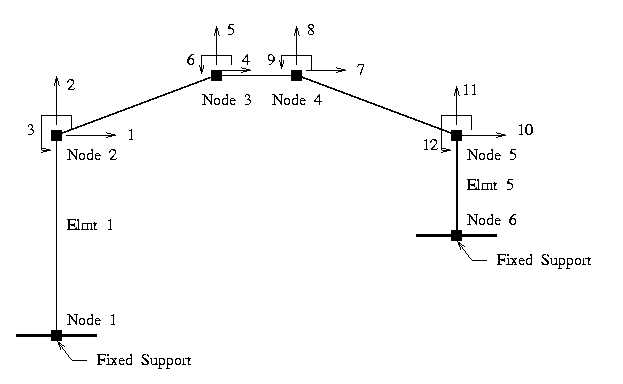
The building supports at nodes 1 and 5 are fully fixed in their translational and rotational degrees of freedom. Nodes 2 through 5 will each be modeled with 2 unknown translational displacements and one unknown rotation. This means that the overall building behavior will be characterized by twelve degrees of freedom.
The block of code:
node = 1; AddNode( node, [ 0 m, 0 m ] ); node = 2; AddNode( node, [ 0 m, 10 m ] ); node = 3; AddNode( node, [ 8 m, 13 m ] ); node = 4; AddNode( node, [ 12 m, 13 m ] ); node = 5; AddNode( node, [ 20 m, 10 m ] ); node = 6; AddNode( node, [ 20 m, 5 m ] );
adds the five nodes to the Aladdin database. A simple looping construct:
elmtno = 0;
for ( ii = 1; ii <= 5 ; ii = ii + 1 ) {
elmtno = elmtno + 1;
AddElmt( elmtno, [ elmtno , elmtno + 1 ], "mrfelmt");
}
can now be used to attach finite elements to the nodes.
Section and Material Properties
The section and material properties are:
ElementAttr("mrfelmt") { type = "FRAME_2D";
section = "mrfsection";
material = "mrfmaterial";
}
SectionAttr("mrfsection") { Izz = 6.60e8 mm^4;
Iyy = 6.60e8 mm^4;
area = 4.26e4 mm^2;
}
MaterialAttr("mrfmaterial") { poisson = 0.25;
yield = 275 MPa;
E = 200 GPa;
}
Boundary Conditions
The block of code:
nodeno = 1;
FixNode( nodeno, [ 1, 1, 1 ]);
nodeno = 6;
FixNode( nodeno, [ 1, 1, 1 ]);
applies full-fixity to the left- and right-hand supports (i.e., nodes 1 and 6, respectively).
External Loads
The abbreviated block of code:
nodeno = 2;
NodeLoad( nodeno, [ 5 kN, -4 kN, 0.0 N*m ]);
demonstrates the procedure for specifying external loads -- in this case, the external loads at node 2 are:
Horizontal Force Fx = 5.0 kN,
Vertical Force Fy = -4.0 kN,
Applied Moment Mz = 0.0 N*m.
Once the global stiffness and external load matrices have been formed with:
stiff = Stiff();
eload = ExternalLoad();
the frame displacements can be computed and printed with:
displ = Solve(stiff, eload);
PrintDispl(displ);
The nodal displacements are:
============================================================
Node Displacement
No displ-x displ-y rot-z
============================================================
units m m rad
1 0.00000e+00 0.00000e+00 0.00000e+00
2 -1.66648e-03 -1.39108e-05 -1.29048e-04
3 -5.38502e-04 -3.05289e-03 -2.32416e-04
4 -5.42568e-04 -2.97523e-03 2.68259e-04
5 5.58718e-04 -7.12911e-06 4.99272e-05
6 0.00000e+00 0.00000e+00 0.00000e+00
The command:
PrintStress(displ);
prints the bending moments and axial forces acting on each beam element. The distribution of bending moments is summarized in Figure [3].
Figure [4] shows the external loads and support reactions.
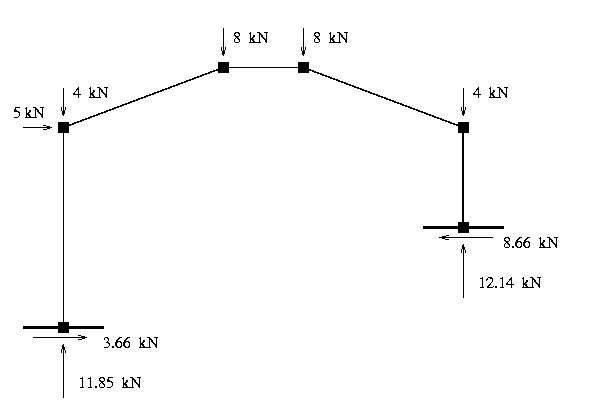
Support Reactions
The command:
actions = GetStress( [1], displ );
retrieves a two by five matrix, actions, containing the x- and y- coordinates of the element nodes, and the horizontal and vertical forces, and moment, acting on each node -- that is:
MATRIX : "actions"
row/col 1 2 3 4 5
units m m N N N.m
1 0.00000e+00 0.00000e+00 1.18520e+04 -3.66177e+03 -1.66054e+04
2 0.00000e+00 1.00000e+01 -1.18520e+04 3.66177e+03 -2.00123e+04
The block of commands:
print "\n";
print "Left-hand Support Reactions\n";
print "===========================\n\n";
print " Vertical Reaction = ", actions[1][3] (kN), "\n";
print "Horizontal Reaction = ", -actions[1][4] (kN), "\n";
print " Moment Reaction = ", actions[1][5] (kN*m), "\n";
extracts the relevant element forces, and generates information on the support reactions:
Left-hand Support Reactions
===========================
Vertical Reaction = 11.85 kN
Horizontal Reaction = 3.662 kN
Moment Reaction = -16.61 kN.m
Of course a similar block of commands can be used to compute and print the right-hand support reactions.
Equilibrium Check
The accuracy of the analysis can be checked by making sure the sum of the column actions -- that is, elements 1 and 5 -- is balanced by the sum of external loads. in the horizontal direction we have:
===============================================================
External Forces Shear Forces in Columns
===============================================================
Joint 2 5,000.0 N
Joint 3 0.0 N
Joint 4 0.0 N Element 1 -3,661.8 N
Joint 5 0.0 N Element 5 8,661.8 N
===============================================================
Total 5,000.0 N 5,000.0 N
===============================================================
And in the vertical direction we have:
===============================================================
External Forces Axial Force in Columns
===============================================================
Joint 2 -4,000.0 N
Joint 3 -8,000.0 N
Joint 4 -8,000.0 N Element 1 -11,852.0 N
Joint 5 -4,000.0 N Element 5 -12,148.0 N
===============================================================
Total -20,000.0 N -20,000.0 N
===============================================================