 Library of Finite Elements
Library of Finite Elements
 Library of Finite Elements
Library of Finite Elements
The finite elements available in Aladdin 1.0 are:
[ 2D Beam-Column Element ]
[ 3D Beam-Column Element ]
[ Plane Stress - Plane Strain Element ]
[ DKQ Plate Element ]
[ Shell Element with Drilling D.O.F. ]
Aladdin 2.0 also supports:
[ 2D Fiber Element ] [ 3D Fiber Element ]
Note : For complete details on the elements in Aladdin 1.0, download Technical Report TR 95-74. A detailed description of the fiber elements can be found in Wane-Jang's Ph.D. dissertation.
Figure 1 shows the two dimensional 2-node frame (or beam/column) element.
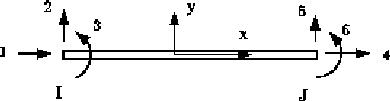
Displacements at each node are modeled with two translational, and one rotational, degree of freedom.
This element may be used for the modeling of linear elastic materials.
Section Properties and Material Properties
The section properties are; Moment of inertia "Izz" and cross-section area -- alternatively, the cross section are is computed from the section width (or bf) times the depth. The material properties are Young's modulus "E", Poisson's ratio "nu", and density "rho."
The element type is FRAME_2D.
Example
end1 = 4*floorno + bayno;
end2 = end1 + 1;
AddElmt( elmtno, [ end1 , end2 ], "mybeam");
....... input code removed ........
ElementAttr("floorbeam") { type = "FRAME_2D";
section = "mysection2";
material = "mymaterial";
}
SectionAttr("floorsection2") { Izz = 1600.3 in^4;
Iyy = 66.2 in^4;
depth = 21.0 in;
width = 8.25 in;
area = 21.46 in^2;
}
MaterialAttr("floormaterial") { density = 0.1024E-5 lb/in^3;
poisson = 0.25;
yield = 36.0 ksi;
E = 29000 ksi;
}
Note : The density may be omitted when a default I-beam section is referenced from the AISC sections header file section.h.
Figure 2 shows the three dimensional 2-node frame (or beam/column) element.
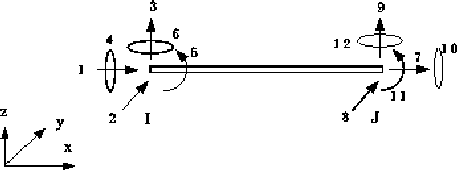
Displacements at each node are modeled with three translational, and three rotational, degrees of freedom.
This element may be used for the modeling of linear elastic materials.
Section Properties and Material Properties
The section properties include moments of inertia "Izz" and "Iyy," and the cross-section "area". The cross-section area may also be computed from the section "depth" times its "width" (or "bf"). The torsional constant and radius of gyration are defined by parameters "J" and "rT", respectively. The material properites are Young's modulus "E", Poisson's ratio "nu", and the density "rho".
The element type is FRAME_3D.
Example
elmtno = 0;
while(elmtno < 4) {
elmtno = elmtno + 1;
AddElmt( elmtno, [elmtno, elmtno + 1], "floorelmt");
}
....... code deleted ....
ElementAttr("floorelmt") { type = "FRAME_3D";
section = "mysection";
material = "mymaterial";
}
SectionAttr("floorsection") { Izz = 13824 in^4;
Iyy = 3456 in^4;
area = 288 in^2;
depth = 24 in;
width = 12 in;
}
MaterialAttr("floormaterial") { .... same as for FRAME_2D example .... }
Note : The density may be omitted when a default I-beam section is referenced from the AISC sections header file section.h.
Figure 3 shows the two dimensional 4-node plane stress/plane strain element.
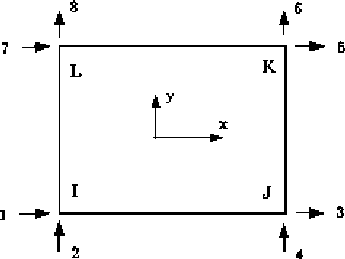
May be used to model linear elastic materials.
Section Properties and Material Properties
Young's modulus "E", Poisson's ratio "nu", Density rho for dynamic analyses; No section properties are needed.
The element type is PLANE_STRESS (or PLANE_STRAIN).
Example
ElementAttr("pipe") { type = "PLANE_STRAIN";
section = "pipesection";
material = "pipematerial"; }
SectionAttr("pipesection") { depth = 30 cm;
width = 30 cm; }
MaterialAttr("pipematerial") { poisson = 1/3;
yield = 36000;
E = 200 GPa; }
Figure 4 shows a four node discrete kirchoff quadrilateral (DKQ) plate element.
Each node has three degrees of freedom -- two rotations, and a lateral displacement.
Section Properties and Material Properties
The section property is plate "thickness". The material properties include Young's modulus "E", and Poisson's ratio "nu".
The element type is DKT_PLATE.
Example
connect = [ 1, 2, 3, 4];
AddElmt( elmtno, connect, "name_of_elmt_attr");
...... input statements removed .....
ElementAttr("name_of_elmt_attr") { type = "DKT_PLATE";
section = "mysection";
material = "ELASTIC";
map ldof [1,2,3] to gdof [2, 4, 6];
}
SectionAttr("mysection") { thickness = 2.0 in; }
MaterialAttr("ELASTIC") { density = 150 lb/ft^3;
poisson = 0.3;
yield = 36000;
E = 29000 psi;
Some working notes:
Note: This element was transformed from FORTRAN to C in the early 1990s by one of my graduate students. If somebody would like to check this work (i.e., check that both versions give identical numerical results). please let me know and I'll get you the appropriate source code.
Figure 5 shows the four node flat shell element with six degrees of freedom per node.

The theoretical formulation of this shell finite element, and numerical examples of its performance may be found in the masters thesis of Lanheng Jin.
This element may be used for modeling of linear elastic materials.
Section Properties and Material Properties
The section attribute is "thickness" alone. The material properties are Young's modulus "E", Poisson's ratio "nu", and Density "rho" (for dynamic analyses). The element has two modeling parameters "ialpha" and "pen".
The element type is SHELL_4NQ.
Example
AddElmt( elmtno+1, [ a+1, b+1, b+2, a+2 ], "bridgegirder" );
..... input code removed .....
ElementAttr("bridgegirder") { type = "SHELL_4NQ";
section = "girder_flange";
material = "STEEL3";
}
SectionAttr( "girder_flange" ) { thickness = 1.100 in; }
Note : STEEL3 is a material property predefined in material.h, and loaded into the ALADDIN database during the program's startup procedure.
Currently, this element does not have a mass matrix.
The fiber element has the same degrees of freedom as the traditional plane frame element.
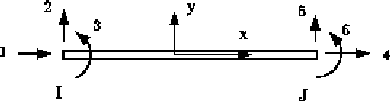
FIBER_2D is the element type name for a two dimensional 2-node fiber element with homogeneous shear properties.
FIBER_2DS is the element type name for a two dimensional 2-node fiber element constructed from fibers having more than one shear property.
Material Properties
The element material properties are defined for the whole element. The material properties include Poisson's ratio "nu" (the default value is 0.3), and "density". The material properties in element type FIBER_2D also include the shear modulus "G", tangent shear modulus "Gt", and shear yield stress "shear_yield". Note that "G", "Gt" and "shear_yield" represent the shear properties for the whole element. Young's modulus "E", tangent Young's modulus "Et" and yield stress "fy" are not defined here -- they will be defined in the fiber attribute instead.
Constituitive Relations
The nonlinear constitutive relations of the overall element cross-section are derived by integration of the nonlinear stress-strain relations of the individual fibers. Each fiber follows a uniaxial stress-strain relation for a particular material. Complex nonlinear section behavior can occur even if the individual fibers are modeled with nonlinear stress-strain relations in the uniaxial direction alone.
The fiber element that we have incorporated into Aladdin 2.0 has a bi-linear stress-strain relationship in uniaxial stress, and follows the kinematic hardening rule shown in Figure 7.
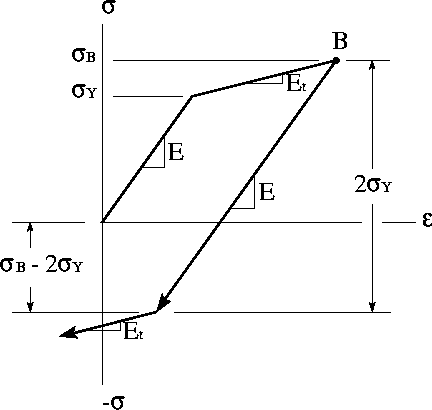
The precise stress-strain relations are defined by three criteria:
d_sigma = E_t depsilon
That is, if the material has yet to yield or is unloading, then sigma = E * depsilon.
Section Properties
The element section properties are defined for the whole element. The section properties include the element's total cross-section area, "area" ("area" may be computed from the section "depth" times its "width" or "bf"). The "shear_factor" for shear effect in the element is 1.2 by default. In order to calculate a mass matrix for dynamic analysis, either "unit_weight" in the section properties, or "density" in the material properties must be supplied. The fiber element supports only lumped mass matrix.
Fiber Attributes
FiberCoordinate includes y-coordinate of each fiber in the element cross section. FiberMaterialAttr includes the Young's modulus, tangent Young's modulus, and yield stress.
Example
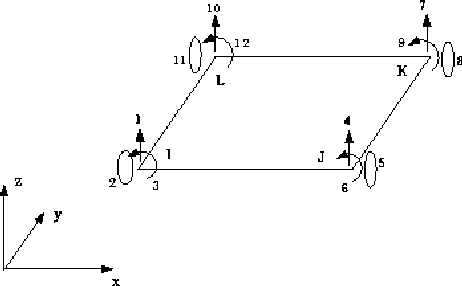
Let's now consider the two-dimensional cross section shown in Figure 8.

The Aladdin statements needed to model the four fiber elements in Figure 7 are:
AddElmt( 1, [1,2], "elmt_attr" );
/* Define element attribute */
ElementAttr("elmt_attr"){ type = "FIBER_2D";
section = "sec_name";
material = "mat_name";
fiber = "fib_name"; }
/* Define section properties */
SectionAttr("sec_name") { area = b*h;
width = b; depth = h;
unit_weight = 1 N/m; }
/* Define material properties */
MaterialAttr("mat_name"){ poisson = nu; G = G; shear_yield = fv; }
/* Element is modeled with 4 fibers and equally meshed. */
no_of_fiber = 4;
fiber_coord = [ 3/8*h, 1/8*h, -1/8*h, -3/8*h ];
fiber_area = [ b*h/4, b*h/4, b*h/4, b*h/4 ];
/* Element is composed of two materials. */
fiber_attr = [ E1, E2;
Et1, Et2;
fy1, fy2 ];
/* Fiber No.1 and No.2 are material 1 */
/* Fiber No.3 and No.4 are material 2 */
fiber_map = [ 1, 1, 2, 2 ];
/* Define Fiber Attribute */
FiberAttr( no_of_fiber, "fib_name" ) { FiberMaterialAttr = fiber_attr;
FiberCoordinate = fiber_coord;
FiberArea = fiber_area;
FiberMaterialMap = fiber_map; }
2D FIBER ELEMENT WITH MULTIPLE SHEAR PROPERTIES
FIBER_2DS is the element type name for a two dimensional 2-node fiber element constructed from fibers having more than one shear property.
The section properties and material properties are the same as FIBER_2D. One exception is that there is now no need to define shear properties in material properties, since they will be defined in FiberMaterialAttr matrix.
Fiber Attribute
FiberMaterialAttr of FIBER_2DS includes the Young's modulus, tangent Young's modulus, yield stress, shear modulus, tangent shear modulus, and shear yield stress.
Example
Here is an example of an element composed of two materials each having their own shear properties:
fiber_attr = [ E1, E2;
Et1, Et2;
fy1, fy2;
G1, G2;
Gt1, Gt2;
fv1, fv2 ];
The three-dimensional fiber element has the same degrees of freedom as the traditional space frame element.

FIBER_3D is the element type name for a three dimensional 2-node fiber element with homogeneous shear properties.
FIBER_3DS is the element type name for a three dimensional 2-node fiber element constructed from fibers having more than one shear property.
Section Properties and Material Properties
The section properties defined here are for the whole element, and include the element's total cross-section "area" ("area" may be computed from the section "depth" times its "width" or "bf"). The "shear_factor" for shear effect in the element is 1.2 by default. The torsional constant "J" has to be given in section properties. For dynamic analysis, in order to calculate mass matrix, "unit_weight" in section properties or "density" in material properties must be given. The fiber element supports only a lumped mass matrix.
The material properties are defined for the whole element, and include mass "density" and Poisson's ratio "nu" ("poisson" is 0.3 by default). The material properties in FIBER_3D also include the shear modulus "G", tangent shear modulus "Gt", and shear yield stress "shear_yield". Note that "G", "Gt" and "shear_yield" represent the shear properties for the whole element. Young's modulus "E", tangent Young's modulus "Et" and yield stress "fy" are not defined here -- they will be defined in fiber attribute instead.
Fiber Attributes
FiberCoordinate defines both y-coordinate and z-coordinate of each fiber in the element cross section. FiberMaterialAttr defines different material types of fibers, it includes the Young's modulus, tangent Young's modulus, and yield stress.
Example
Let's now consider the two-dimensional cross section shown in Figure 10.

The Aladdin statements needed to construct this element are:
AddElmt( 1, [1,2], "elmt_attr" );
/* Define Element Attribute */
ElementAttr("elmt_attr"){ type = "FIBER_3D";
section = "sec_name";
material = "mat_name";
fiber = "fib_name"; }
/* Define Section Properties */
SectionAttr("sec_name") { area = b*h;
width = b; depth = h;
J = 0.2 m^4;
unit_weight = 1 N/m; }
/* Define Material Properties */
MaterialAttr("mat_name"){ poisson = nu; G = G; shear_yield = fv; }
/* Element is modeled with 8 fibers and equally meshed. */
/* (4 rows by 2 columns) of fibers per cross section */
no_of_fiber = 2*4;
fiber_coord=[ b/4, -b/4, b/4, -b/4, b/4, -b/4, b/4, -b/4];
3/8*h, 3/8*h, 1/8*h, 1/8*h, -1/8*h, -1/8*h, -3/8*h, -3/8*h];
fiber_area =[b*h/8, b*h/8, b*h/8, b*h/8, b*h/8, b*h/8, b*h/8, b*h/8];
/* Element is composed of two materials. */
fiber_attr = [ E1, E2;
Et1, Et2;
fy1, fy2 ];
/* Fiber No.1 to No.4 are material 1 */
/* Fiber No.5 to No.8 are material 2 */
fiber_map = [ 1, 1, 1, 1, 2, 2, 2, 2 ];
/* Define Fiber Attribute */
FiberAttr( no_of_fiber, "fib_name" ) { FiberMaterialAttr = fiber_attr;
FiberCoordinate = fiber_coord;
FiberArea = fiber_area;
FiberMaterialMap = fiber_map; }
3D FIBER ELEMENT WITH DIFFERENT SHEAR PROPERTIES
FIBER_3DS is the element type name for a three dimensional 2-node fiber element constructed from fibers having more than one shear property.
The section properties and material properties are the same as FIBER_3D, except that there is no need to define shear properties in material properties; they will be defined in FiberMaterialAttr matrix.
Fiber Attributes
FiberMaterialAttr of FIBER_3DS includes the Young's modulus, tangent Young's modulus, yield stress, shear modulus, tangent shear modulus, and shear yield stress.
Example
Here is an example of an element composed of two materials having their own shear properties:
fiber_attr = [ E1, E2;
Et1, Et2;
fy1, fy2;
G1, G2;
Gt1, Gt2;
fv1, fv2 ];
Developed in July 1996 by Mark Austin
Copyright © 1996-2000, Department of Civil Engineering, University of Maryland